

REACTIVO LÍMITE
MASA,
PESO Y VOLUMEN
La masa
es la cantidad de materia que contiene un cuerpo y el peso es
la acción que ejerce la fuerza de gravedad sobre el cuerpo.
La masa de un objeto siempre será
la misma, sin importar el lugar donde se ubica. En cambio, el peso del objeto
variará de acuerdo a la fuerza de gravedad que actúa sobre este.
Por ejemplo: una persona con una
masa de 50 kg en la Tierra tendrá la misma masa en la Luna. Por otro lado, el
peso de esa misma persona será 6 veces menor en el satélite con respecto a la
del planeta debido a las diferencias en la fuerza de la gravedad. La fuerza de
gravedad en la Luna es de 1,622 m/s2 y en la Tierra es de 9,8 m/s2.
|
Masa (m) |
Peso (p) |
|
Es una magnitud escalar. |
Es una magnitud vectorial. |
|
Es la cantidad de materia que tiene un cuerpo. |
Es la acción que ejerce la fuerza de gravedad. |
|
Su valor es constante. |
Su valor varía según la posición. |
|
Se mide con la balanza. |
Se mide con el dinamómetro. |
|
Unidad de medida: kilogramo (Kg) y gramo (g). |
Unidad de medida: Newton (N). |
|
Cantidad intrínseca. |
Cantidad extrínseca. |
¿Qué es la masa?
La masa es la cantidad de materia
que un objeto posee. Es una medida cuantitativa de la resistencia a la
aceleración de un cuerpo. Lo podemos ver como la resistencia de una vajilla en
la mesa cuando se saca de un tirón el mantel.
Independientemente del lugar en
donde se encuentra el cuerpo, la masa siempre será igual, es decir, es una
cantidad intrínseca de la materia.
La masa es una propiedad
extensiva de la materia, depende de la cantidad y del tamaño del sistema en
estudio. Esto significa que si un objeto de masa igual 1 kg, le quitamos 0,1
kg, ya la masa no será igual en el objeto original.
¿Cómo se mide la masa?
La masa se mide normalmente por
medio de una balanza, haciendo una comparación con un estándar conocido. En el
Sistema Internacional de Unidades (SI) la masa se expresa en kilogramo (kg).
Desde el 20 de mayo del 2019 el kilogramo se define en términos de la constante
de Planck h, una constante fundamental de la física cuántica que es
universal:
Esta nueva medida del kilogramo
reemplaza la antigua definición del kilogramo, basada en el prototipo
de kilogramo internacional, un cilindro de platino e iridio que se mantiene
resguardado en el Bureau Internacional de Pesos y Medidas en Sèvres, Francia en
1889.
¿Qué es el peso?
El peso es la fuerza
gravitacional ejercida por la Tierra o cualquier otro cuerpo celeste sobre un
objeto, que es igual al producto de la masa del objeto y el valor de la
aceleración gravitacional local:
P= m x g
El valor de la constante de
aceleración en la Tierra es 9,8 m/s2. Por la fórmula se puede interpretar que el peso
es proporcional a la masa del objeto.
El peso es una magnitud vectorial
ya que posee intensidad, dirección y sentido. Como tal, el peso es una medida
resultante de la acción que ejerce la gravedad terrestre sobre un cuerpo, y de
esta forma, el peso es un valor variable.
¿Cómo se mide el peso?
El instrumento que se usa para
determinar el peso es el dinamómetro o balanza de resorte. Esto consiste en un
resorte espiral protegido que mide la fuerza que se aplica al final de un
puntero.
En el Sistema Internacional de
Unidades (SI), la unidad del peso se expresa en Newton (N), que es igual a:
EL
VOLUMEN
El
volumen corresponde a la medida del espacio que ocupa un cuerpo. La unidad de
medida para medir volumen es el metro cubico (m3), sin
embargo, generalmente se utiliza el Litro (L). El
metro cubico corresponde a medir las dimensiones de un cubo que mide 1 m de
largo, 1 m de ancho y 1 m de alto.
La temperatura influye
directamente sobre el volumen de los gases y los líquidos
§ Si la
temperatura aumenta, los sólidos y los líquidos se dilatan.
§ Si la
temperatura disminuye, los sólidos y los líquidos se contraen.
§
Medición de Volumen
Existen variadas formas de medir volúmenes. Para
medir el volumen de un líquido se pueden utilizar instrumentos como un vaso
precipitado, probeta, pipeta, matraces, entre otros.
Instrumentos para medir volumen (Probetas).
Para
medir el volumen de un sólido irregular, se puede utilizar el método por
inmersión en agua. Así el volumen del solido será la diferencia entre el
volumen final, que se mide cuando el objeto está dentro de una probeta, menos
el volumen inicial.
Para medir el volumen de un
sólido geométrico se suelen utilizar fórmulas matemáticas. Por ejemplo, para
medir el volumen de una esfera, un cubo, o un cilindro se utilizan las
siguientes formulas.
Fórmulas para medir volúmenes de sólidos regulares.
D=m/v
EJEMPLO:
Un cubo de metal tiene una arista de 5cm, si su peso es de
352g ¿cuál es la densidad del metal?
d=?
m= 352g
v= 125cm3
arista cubo= 5cm
HALLAR VOLUMEN DEL CUBO
lado= arista
V cubo = lado x lado x lado
V cubo= 5cm x 5cm x 5cm = 125cm3
d= m/ v d=
352g/125cm3 = 2.8g/cm3 densidad del metal
Para hallar el volumen:
v= m/d
para hallar la masa:
m= d x v
ejemplos:
¿Cuál es el volumen de una sustancia que tiene una masa 150g
y una densidad de 0.75g/cm3?
v= m / d
v= 150 g / 0.75 g/cm3
v= 200cm3
¿Cuál es la masa de una sustancia que ocupa un espacio de
345ml y tiene una densidad de 1.25g/cm3?
m= d x v
m= 1.25g/cm3 x 345cm3
m= 431.25g
ACTIVIDAD GRADO 10-1
1.
Sabiendo que la densidad del aluminio es 2,7
g/cm3, ¿cuál es la masa de una esfera de aluminio de 50 cm3?
2.
La densidad de un alcohol es 0.8 g/cm3.
Calcular el volumen de 2500 g de alcohol.
3.
Si 1cm3 de Mercurio pesa 13,6 g.
¿Cuál es la masa de un cilindro de r= 2.5 cm y altura: 10cm?
4.
Un cubo sólido mide 6.0 cm en cada lado y tiene
una masa de 650g. ¿Cuál es su densidad en g/cm3
ACTIVIDAD GRADO 10-2
1.
Un bloque de aluminio con una densidad de 2.70
g/cm3 tiene masa de 777.5 g ¿Cuál es el volumen del bloque?
2.
Una pequeña piedra tiene una masa de 60 g. la
piedra es colocada en una probeta que contiene agua. El nivel del agua en la
probeta cambia de 25 ml a 45 ml cuando la piedra se sumerge. ¿Cuál es la
densidad de la piedra?
3.
Para determinar el volumen de leche que lleva un
carro tanque se procedió así:
- Se pesó el camión vació y su
masa fue de 26100 kg
- Se llenó el camión con leche
(densidad de la leche 1200 kg/m3) y se pesó, obteniéndose un valor de pesada de
35966 kg.
¿Es posible determinar el volumen
de leche? cuál es?
INTERPRETACIÓN DE ECUACIONES BALANCEADAS: ESTEQUIOMETRÍA
NOTACIÓN CIENTÍFICA
La notación científica nos permite escribir números muy grandes o muy pequeños de forma abreviada. Esta notación consiste simplemente en multiplicar por una potencia de base 10 con exponente positivo o negativo.
Ejemplo: el número 0,00000123 puede escribirse en notación científica como
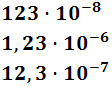
Evitamos escribir los ceros decimales del número, lo que facilita tanto la lectura como la escritura del mismo, reduciendo la probabilidad de cometer erratas.
Obsérvese que existen múltiples posibilidades de expresar el mismo número, todas ellas igualmente válidas.
Recordatorio del significado y valor de las potencias de base 10 con exponente positivo y con exponente negativo.
Si n es positivo, la potencia de base 10 con exponente n, es decir, 10n, es el número formado por la cifra 1 seguida de n ceros.
Ejemplo:
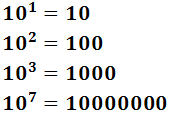
El exponente indica el número de 0's.
La potencia de base 10 con exponente negativo -n, es decir, 10-n, es el número decimal 0,00...01 siendo n el número total de ceros.
Ejemplo:
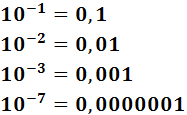
El exponente indica el número de 0's, contabilizando también el cero situado a la izquierda de la coma.
La notación científica consiste precisamente en multiplicar por una potencia de 10. En esta sección explicamos el resultado de multiplicar o dividir un número por 10 para comprender el resultado de multiplicar por una potencia
Al multiplicar un número por 10, su coma decimal se desplaza una posición hacia la derecha (si no tiene coma, se escribe un 0 a la derecha de la última cifra).
Ejemplo:

Al multiplicar el número decimal 12,5 por 10, la coma se desplaza una posición hacia la derecha. Como detrás de la coma sólo hay ceros, podemos omitirla.
Al multiplicar el número natural (no decimal) 123 por 10, tenemos que añadirle un 0 a la derecha.
Al dividir un número entre 10, su coma decimal se desplaza una posición hacia la izquierda (si no tiene coma, se introduce a la izquierda de la primera cifra).
Ejemplo:
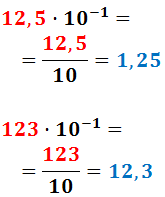
Al dividir el número decimal 12,5 entre 10, la coma se desplaza una posición hacia la izquierda.
Al dividir el número natural (no decimal) 123 entre 10, tenemos que añadirle una coma.
Importante: dividir entre 10 es lo mismo que multiplicar por la potencia de exponente negativo 10-1.
En el apartado anterior vimos que al multiplicar un número por 10 la coma decimal de dicho número se desplaza una posición hacia la derecha.
Como multiplicar sucesivamente (varias veces) por 10 es lo mismo que multiplicar por una potencia de 10,
Al multiplicar un número por la potencia 10n (con exponente positivo) se desplaza la coma hacia la derecha tantas posiciones como indica el exponente.
Ejemplo:
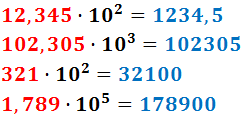
Como los exponentes son positivos, la coma se desplaza hacia la derecha.
Si no hay suficientes cifras para desplazar la coma, se añaden 0's (a la derecha).
Anteriormente vimos que al dividir un número entre 10 la coma decimal de dicho número se desplaza una posición hacia la izquierda.
Como dividir sucesivamente (varias veces) entre 10 es lo mismo que multiplicar por una potencia de 10 con exponente negativo,
Al multiplicar un número por la potencia 10-n (con exponente negativo) se desplaza la coma hacia la izquierda tantas posiciones como indica el exponente (al cambiarle el signo).
Ejemplo:
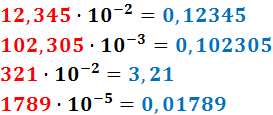
Como los exponentes son negativos, la coma se desplaza hacia la izquierda.
Si no hay suficientes cifras para desplazar la coma, se añaden 0's (a la izquierda). Esto ocurre en el primer, segundo y cuarto número del ejemplo.
Nota: el número resultante al cambiar el signo del exponente indica cuántas posiciones se desplaza la coma:
10-2: dos posiciones hacia la izquierda.
10-3: tres posiciones hacia la izquierda.
10-2: dos posiciones hacia la izquierda.
10-5: cinco posiciones hacia la izquierda.
ACTIVIDAD
1.
Escribir los siguientes números en notación
científica:
a)
4535000000000000000000000
b)
0.000000000000000032154
2.
Escribir el número decimal
a)
0.672 X 1014
b)
4,5678 X 10-24
ACTIVIDAD PROYECTO DE VIDA GRADO 10-1 FECHA DE ENTREGA: Lunes 26 de abril de 2021 Objetivo: identificar y aprender a modificar los pensami...
